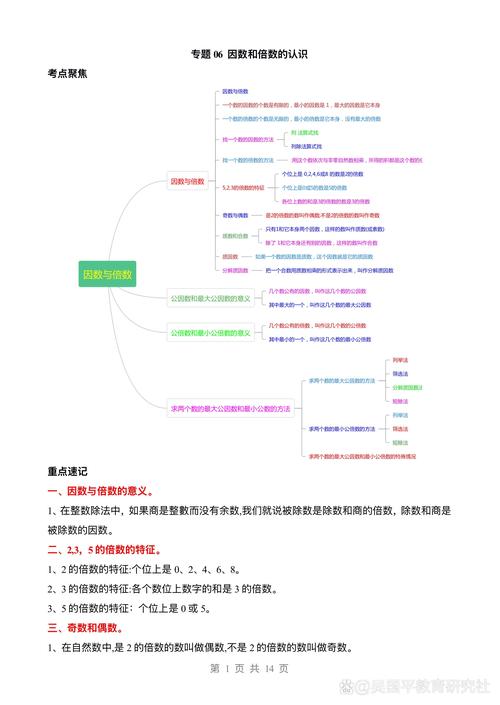
什么是“数学思维”?
它不是指背公式、刷题海,而是一种底层的思考方式和能力,核心包括:
- 逻辑推理能力: 从已知条件出发,通过严谨的推导,得出结论,因为.....”的链条。
- 抽象概括能力: 从具体问题中提炼出数学模型(比如用数字、字母、图形表示),比如看到3个苹果和2个梨,能抽象出“3+2”。
- 空间想象能力: 在脑海中构建和操作二维、三维图形的能力,比如几何题、折纸、搭积木。
- 模式识别能力: 发现事物中隐藏的规律和模式,比如数列 2, 4, 6, 8, ? 的规律是“+2”。
- 转化与化归能力: 将一个复杂或陌生的问题,转化为一个简单或熟悉的问题来解决,比如将求不规则图形的面积,转化为求几个规则图形的面积之和。
- 模型思想: 将现实生活中的问题,用数学语言(方程、函数、不等式等)来描述和解决。
如何进行有效的数学思维辅导?(袁辅导可能会这样做)
优秀的数学思维辅导,绝不是简单地告诉孩子“答案是什么”,而是引导孩子思考“为什么”和“怎么办”。
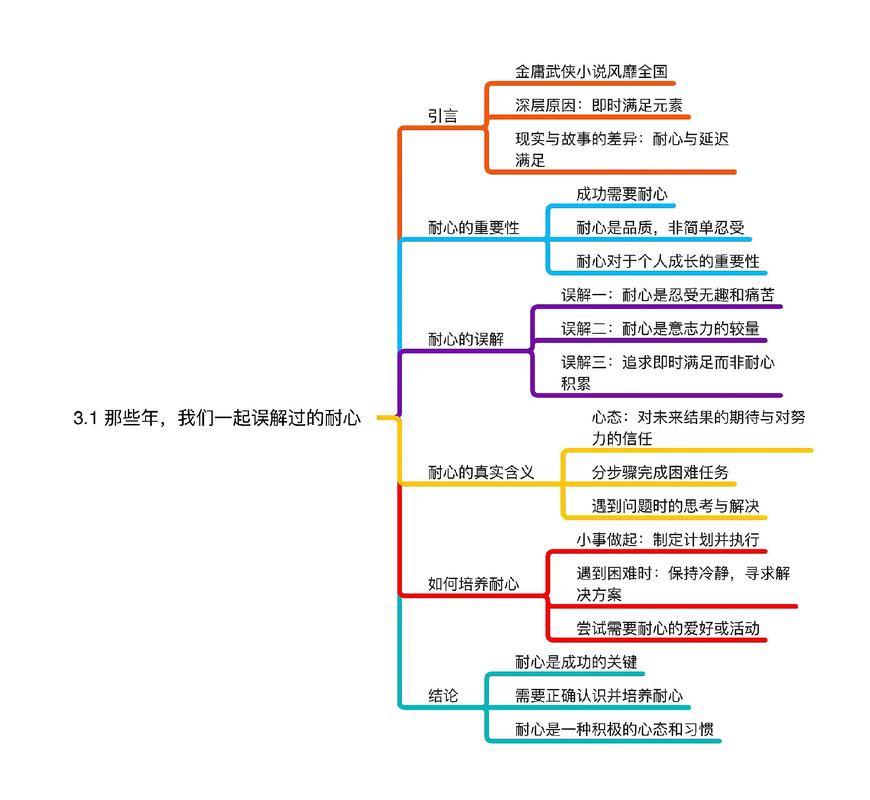
兴趣是最好的老师(低年级)
- 生活化: 把数学融入生活,去超市购物时让孩子算价格;切蛋糕时认识分数;搭积木时学习立体几何。
- 游戏化: 使用棋盘、扑克牌、数独、魔方等工具,在玩乐中锻炼逻辑和计算能力。
- 故事化: 用有趣的故事引入数学问题,小熊分蜂蜜”引出除法概念。
建立思考的“脚手架”(中年级)
这个阶段开始接触更抽象的概念,重点是理解过程,而非死记硬背。
- 一题多解: 鼓励孩子用不同的方法解决同一个问题,比如计算 25x4,可以拆成 (20+5)x4,也可以看成 100,这能极大地锻炼思维的灵活性。
- 追问“为什么”: 当孩子说出答案时,老师或家长要追问:“你是怎么想到的?”“还有别的方法吗?”“如果条件变了,结果会怎样吗?”
- 画图辅助: “数形结合”是数学思维的精髓,遇到复杂的应用题,引导孩子画线段图、示意图,把抽象的数量关系变得直观。
- 鼓励错误: 错误是宝贵的思考资源,和孩子一起分析错误的原因,是概念不清?还是计算失误?这比直接给正确答案更有价值。
培养高阶思维(高年级及以上)
这个阶段要挑战孩子的思维深度和广度,为解决复杂问题做准备。
- 专题训练: 针对性地进行专题训练,如“鸡兔同笼”、“行程问题”、“逻辑推理”等,掌握特定问题的模型和解题策略。
- 开放性问题: 提出没有唯一标准答案的问题,如何用一张A4纸撑起一本书?”,鼓励孩子大胆假设、小心求证。
- 数学建模: 尝试解决一些“伪”实际问题,如何规划一次班级秋游,使得最省钱?”让孩子体验从实际问题到数学模型的完整过程。
- 拓展阅读: 鼓励孩子阅读《数学之美》、《从一到无穷大》等科普读物,感受数学的魅力和广度。
给家长的建议(如何配合“袁辅导”)
- 心态调整: 认识到数学思维培养是“慢功夫”,不要急于求成,不要用分数作为唯一衡量标准,保护孩子的好奇心和自信心最重要。
- 多问少说: 在辅导孩子时,尽量扮演“引导者”和“提问者”的角色,而不是“答案提供者”,多用“你觉得呢?”“我们试试看?”这样的句式。
- 创造环境: 在家里营造一个可以自由讨论、不怕犯错的家庭氛围,当孩子遇到难题时,和他一起坐下来,像侦探一样寻找线索。
- 与老师沟通: 定期与“袁辅导”沟通,了解孩子在课堂上的表现和思维特点,家校配合,才能形成合力。
“袁辅导数学思维”的核心,应该是“授人以渔”,即传授思考的方法,而不是“授人以鱼”(直接给答案),一个好的数学思维辅导,能让孩子:
- 不怕难题:因为他们有分析和拆解问题的方法。
- 享受思考:因为他们能从逻辑推理和解决问题中获得乐趣。
- 终身受益:数学思维是学习任何学科、解决任何问题的基础。
希望这份梳理能对您有所帮助!如果您有更具体的问题,比如某个年级、某个知识点,我们可以继续深入探讨。