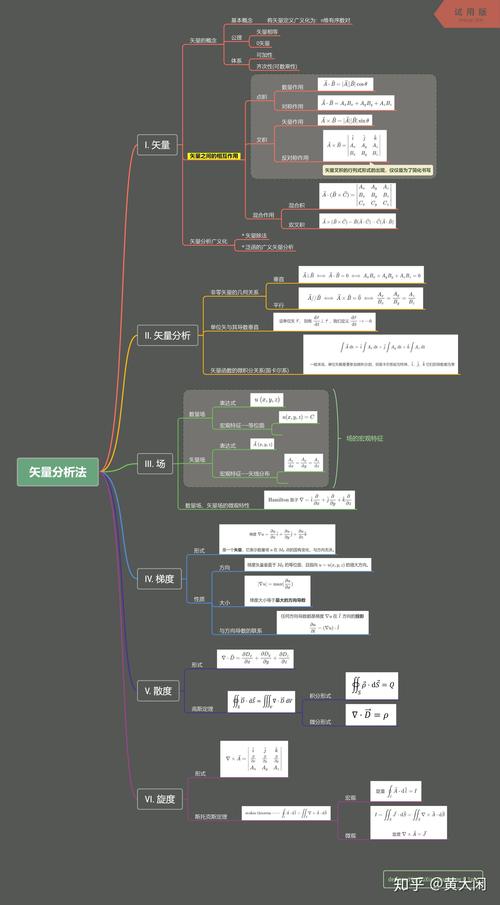
第一部分:课程宏观框架与核心思想
不要被“矢量”、“场”、“微分”、“积分”这些名词吓到,这门课的核心目标是用数学工具描述和分析物理空间中的各种“场”。
你可以把这门课想象成三个层次的递进:

- 描述(是什么?): 如何用数学语言(矢量、标量)来描述空间中一个点的某种属性(如温度、速度、电场强度)。
- 变化(怎么样?): 这个属性在空间中是如何变化的?它变化得有多快?变化的方向是什么?
- 关系(为什么?): 这种变化背后遵循什么规律?如何通过一个区域的整体信息来推断其边界上的信息,反之亦然?
核心思想:微积分在多维空间中的推广。
- 一元微积分: 研究一维数轴上的函数
y = f(x),核心是dy/dx(变化率)和∫f(x)dx(求和)。 - 矢量分析与场论: 研究三维空间中的场
F = F(x, y, z),核心是梯度、散度、旋度(这三种“导数”)和线积分、面积分、体积分(这三种“积分”)。
第二部分:核心概念精讲(三大“导数”)
这是整个课程的基石,必须深刻理解它们的物理意义和几何意义。
梯度
- 对象: 一个标量场
u(x, y, z),温度场T(x, y, z)、电势场φ(x, y, z)。 - 定义:
grad(u) = ∇u = (∂u/∂x)i + (∂u/∂y)j + (∂u/∂z)k - 几何意义: 一个矢量,在任意一点,它的方向是标量场
u变化率最快的方向,它的模(长度)是这个最大变化率的值。 - 物理意义: 标量场
u的“陡峭程度”和“方向”。- 在温度场中,某点的梯度方向指向温度升高最快的方向。
- 在电势场中,
E = -∇φ,电场强度的方向是电势降低最快的方向。
- 关键点: 梯度始终垂直于等值面(如等温面、等势面)。
散度
- 对象: 一个矢量场
F(x, y, z),流速场v(x, y, z)、电场强度E(x, y, z)。 - 定义:
div(F) = ∇ · F = ∂F_x/∂x + ∂F_y/∂y + ∂F_z/∂z - 几何意义: 一个标量,它衡量了矢量场
F在某一点的“源”或“汇”的强度。∇ · F > 0:该点是一个源(流体喷出、电场线发出)。∇ · F < 0:该点是一个汇(流体吸入、电场线汇聚)。∇ · F = 0:该点既不是源也不是汇(场线只是通过)。
- 物理意义: 描述场的“产生”或“消失”的局部性质,在无电荷区域,
∇ · E = 0,意味着电场线不会在这一点中断或产生。
旋度
- 对象: 一个矢量场
F(x, y, z),流速场v(x, y, z)、磁场B(x, y, z)。 - 定义:
curl(F) = ∇ × F = | i j k || ∂/∂x ∂/∂y ∂/∂z || F_x F_y F_z | - 几何意义: 一个矢量,它的方向与矢量场
F在该点“旋转”的轴向相同(遵循右手定则),它的模表示旋转的剧烈程度。 - 物理意义: 描述场的“旋转”或“涡旋”的局部性质,在流体中,旋度不为零的点就是有涡旋的地方,在电磁学中,
∇ × E = -∂B/∂t描述了变化的磁场会产生涡旋电场。
第三部分:核心定理(三大“积分定理”)
这些定理是连接“局部变化”与“整体性质”的桥梁,是解决问题的关键。
高斯定理(散度定理)
- 公式:
∯_S F · dS = ∭_V (∇ · F) dV - 解读: 矢量场
F穿过任意闭合曲面S的通量(整体性质),等于该矢量场的散度在S所包围的体积V内的体积分(局部性质)。 - 核心: 将面积分转化为体积分。
- 应用: 计算复杂闭合曲面的通量;从物理上理解散度的含义(源的总强度等于流出闭合面的总通量)。
斯托克斯定理
- 公式:
∮_C F · dr = ∬_S (∇ × F) · dS - 解读: 矢量场
F沿任意闭合曲线C的环量(整体性质),等于该矢量场的旋度在以C为边界的任意曲面S上的通量(局部性质)。 - 核心: 将线积分转化为面积分。
- 应用: 计算复杂闭合路径的环量;从物理上理解旋度的含义(涡旋的总强度等于沿路径的环量)。
格林公式
- 可以看作是高斯定理和斯托克斯定理在二维平面上的特例。
- 格林第一公式:
∬_D (u∇²v + ∇u·∇v) dσ = ∮_∂D u(∇v)·n ds - 格林第二公式:
∬_D (u∇²v - v∇²u) dσ = ∮_∂D (u∇v - v∇u)·n ds - 核心: 连接了区域
D内的积分与其边界∂D上的积分,在求解二维 Laplace 方程或 Poisson 方程的边值问题中非常重要。
第四部分:常见难点与学习建议
难点1:符号混淆与计算错误
- 问题: 既是微分算符,又像矢量,可以点乘、叉乘,容易混淆,行列式形式的旋度计算容易出错。
- 建议:
- 区分符号: 明确
∇u(梯度,矢量)、∇·F(散度,标量)、∇×F(旋度,矢量)。 - 动手计算: 多做练习,特别是旋度的行列式展开,确保公式记牢。
- 检查量纲: 计算后检查结果的物理量是否正确(梯度是“场/长度”,散度是“场/长度”,旋度是“场”)。
- 区分符号: 明确
难点2:物理意义与几何意义理解不深
- 问题: 只会背公式,但不知道它到底代表什么,看到题目不知道该用梯度、散度还是旋度。
- 建议:
- 联想物理实例: 学完一个概念,立刻想它在电磁学或流体力学中的对应物。
- ->
E ∇·E->∇×B->J + ε₀∂E/∂t
- ->
- 画图!画图!画图! 画出等值面、矢量场线、涡旋示意图,几何直观是理解抽象概念的最好工具。
- 联想物理实例: 学完一个概念,立刻想它在电磁学或流体力学中的对应物。
难点3:积分定理的应用
- 问题: 面对一个复杂的积分,不知道该用哪个定理,或者不知道如何选择合适的曲面/体积。
- 建议:
- 观察积分形式:
- 积分域是闭合曲面? -> 优先考虑高斯定理。
- 积分域是闭合曲线? -> 优先考虑斯托克斯定理。
- 化繁为简: 定理的威力在于将复杂的曲面积分/线积分,转化为相对简单的体积分/面积分,选择一个能让被积函数变得简单的积分域。
- 灵活运用: 有时即使积分域不闭合,也可以通过“补上一个面”使其闭合,然后用定理减去补上的那个面的积分。
- 观察积分形式:
第五部分:典型例题与练习方向
例题1:梯度与等值面
已知标量场 u(x, y, z) = x² + y² + z²。

- 求
u在点P(1, -1, 2)的梯度。 - 求
u在点P沿方向l = (2, -1, 0)的方向导数。 - 指出
u的等值面u=6在点P的切平面方程。
解析:
∇u = (2x, 2y, 2z),在P(1, -1, 2)点,∇u|_P = (2, -2, 4)。- 方向
l的单位矢量l₀ = (2/√5, -1/√5, 0),方向导数为∇u|_P · l₀ = (2)(2/√5) + (-2)(-1/√5) + (4)(0) = 6/√5。 - 梯度
(2, -2, 4)是切平面的法矢量,切平面方程为2(x-1) - 2(y+1) + 4(z-2) = 0。
例题2:高斯定理的应用
计算矢量场 F = (x³, y³, z³) 穿过立方体 0 ≤ x, y, z ≤ a 的表面的通量。
解析:
直接计算六个面的通量非常繁琐,使用高斯定理:
∯_S F · dS = ∭_V (∇ · F) dV
∇ · F = ∂(x³)/∂x + ∂(y³)/∂y + ∂(z³)/∂z = 3x² + 3y² + 3z² = 3(x² + y² + z²)
∭_V 3(x² + y² + z²) dV = 3 ∫₀ᵃ ∫₀ᵃ ∫₀ᵃ (x² + y² + z²) dx dy dz
通过对称性计算,可得结果为 3a⁵,这比直接计算面积分简单得多。
例题3:斯托克斯定理的应用
计算矢量场 F = (-y, x, 0) 沿圆 C: x² + y² = R², z = 0 的环量。
解析:
- 直接计算(线积分): 参数化
C: x = Rcosθ, y = Rsinθ, z = 0。dr = (-Rsinθdθ, Rcosθdθ, 0)。F = (-Rsinθ, Rcosθ, 0)。F · dr = R²sin²θdθ + R²cos²θdθ = R²dθ,环量∮_C F · dr = ∫₀²π R²dθ = 2πR²。 - 用斯托克斯定理(面积分):
∮_C F · dr = ∬_S (∇ × F) · dS。∇ × F = | i j k | = (0, 0, 2)- 选择
S为圆盘x² + y² ≤ R², z = 0,其法矢量dS = (0, 0, 1)dxdy。 ∬_S (0, 0, 2) · (0, 0, 1)dxdy = ∬_S 2 dxdy = 2 * (圆盘面积) = 2 * πR² = 2πR²。 结果一致,验证了定理。
第六部分:学习路径建议
- 打好基础: 确保你非常熟悉矢量的点积、叉积以及多元函数的偏导数。
- 概念先行: 先理解梯度、散度、旋度的物理和几何意义,再进行计算。
- 定理为王: 重点掌握高斯定理和斯托克斯定理的证明思路、条件和应用场景,它们是考试的难点和重点。
- 精做习题: 不要盲目刷题,做一道题,就要搞懂它用到了哪个概念,为什么用这个定理,有没有其他解法。
- 联系实际: 如果你是物理或工程专业,一定要把矢量分析与《电磁学》或《流体力学》结合起来学,你会发现很多公式和定理是直接对应的,理解会事半功倍。
如果你在具体某个知识点(比如哈密顿算子 的运算法则、正交曲线坐标系、或某个特定题目)上还有疑问,随时可以提出来,我们可以进行更深入的探讨!











